Pada
tulisan ini saya akan membagikan sidikit ilmu yang saya dapat tentang
bagaimana cara menghitung determinan matriks. Metode yang digunakan
adalah menggunakan Ekspansi Kofaktor. Metode ini tidak
hanya digunakan untuk menghitung determinan matriks 2×2 atau 3×3 tapi
digunakan untuk matriks yang berordo lebih besar lagi seperti, 4×4, 5×5
dan seterusnya. Untuk menghitung determinan menggunakan metode ini,
rumusnya dijamin oleh Teorema berikut.
Teorema :
Determinan
matriks A yang berukuran n x n dapat dihitung dengan mengalikan
entri-entri dalam suatu baris (atau kolom) dengan kofaktor-kofaktornya
dan menambahkan hasil-hasil kali yang dihasilkan yakni untuk setiap 1  i
i  n dan 1
n dan 1  j
j  n, maka
n, maka
det(A) = a1jC1j + a2jC2j + … + anjCnj
(ekspansi kofaktor sepanjang kolom ke-j)
atau
det(A) = ai1Ci1 + ai2Ci2 + … + ainCin
(ekspansi kofaktor sepanjang baris ke-i)
Untuk lebih memperjelas apa itu kofaktor, perhatikan Definisi dibawah ini.
Definisi :
Jika A adalah matriks kuadrat, maka minor entri aij dinyatakan oleh Mij dan didefinisikan menjadi determinan submatriks yang tetap setelah baris ke-i dan kolom ke-j dicoret dari A. Bilangan (-1)i+jMij dinyatakan oleh Cij dan dinamakan kofaktor entri aij.
Contoh 1 :
Misalkan kita punya matriks A = ![\left [ \begin{array}{rrr} 3& 1& -4\\ 2& 5& 6\\ 1& 4& 8 \end{array} \right ] \left [ \begin{array}{rrr} 3& 1& -4\\ 2& 5& 6\\ 1& 4& 8 \end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brrr%7D+3%26+1%26+-4%5C%5C+2%26+5%26+6%5C%5C+1%26+4%26+8+%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) . Tentukan minor entri a11, a12, dan a13. Tentukan juga kofaktor entri M11, M12 dan M13 !
. Tentukan minor entri a11, a12, dan a13. Tentukan juga kofaktor entri M11, M12 dan M13 !
Penyelesaian :
minor entri a11 adalah M11 =  =
=  = 5(8) – 4(6) = 16
= 5(8) – 4(6) = 16
kofaktor a11 adalah C11 = (-1)1+1M11 = (-1)2(16) = 16
minor entri a12 adalah M12 =  =
=  = 2(8) – 1(6) = 10
= 2(8) – 1(6) = 10
kofaktor a12 adalah C12 = (-1)1+2M12 = (-1)3(10) = -10
minor entri a13 adalah M13 =  =
=  = 2(4) – 1(5) = 3
= 2(4) – 1(5) = 3
kofaktor a13 adalah C13 = (-1)1+3M13 = (-1)4(3) = 3
Contoh 2 :
Dari Contoh 1 diatas, tentukan determinan matriks A
Penyelesaian :
Menggunakan yang diberikan pada Teorema diatas dengan mengambil i = 1 dan j = 1, 2, dan 3, maka diperoleh.
det(A) = a11C11 + a12C12 + a13C13
= 3(16) + 1(-10) + (-4)(3)
= 48 – 10 – 3
= 35
Contoh 3 :
Tentukan determinan matriks A = ![\left [ \begin{array}{rrr} 0& 6& 0\\ 8& 6& 8\\ 3& 2& 2 \end{array} \right ] \left [ \begin{array}{rrr} 0& 6& 0\\ 8& 6& 8\\ 3& 2& 2 \end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brrr%7D+0%26+6%26+0%5C%5C+8%26+6%26+8%5C%5C+3%26+2%26+2+%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
Penyelesaian :
Menggunakan yang diberikan pada Teorema diatas dengan mengambil i = 3 dan j = 1, 2, dan 3, maka diperoleh.
det(A) = 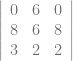
= a31C31 + a32C32 + a33C33
= a31(-1)3+1M31 + a32(-1)3+2M31 + a33(-1)3+3M31
= a31M31 – a32M31 + a33M31
= 3 – 2
– 2 + 2
+ 2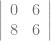
= 3[6(8)-0(6)] – 2[0(8)-8(0)] + 2[0(6)-8(6)]
= 144 – 0 – 96
= 48
atau
jika ingin lebih cepat, kita bisa melihat entri yang mengandung nol
agar lebih mempersingkat waktu mengerjakan. Karena dalam baris pertama
terdapat dua entri nol, maka i = 1 dan j = 1, 2, 3 kemudian gunakan
rumus.
det(A) = a11C11 + a12C12 + a13C13
= a11(-1)1+1M11 + a12(-1)1+2M12 + a13(-1)1+3M13
= a11M11 – a12M12 + a13M13
= 0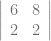 – 6
– 6 + 0
+ 0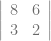
= 0 – 6[8(2)-8(3)] + 0
= 48
Contoh 4 :
Tentukan determinan matriks B = ![\left [ \begin{array}{rrrr} 2& 1& 3& 1\\ 1& 0& 1& 1\\ 0& 2& 1& 0\\ 0& 1& 2& 3 \end{array} \right ] \left [ \begin{array}{rrrr} 2& 1& 3& 1\\ 1& 0& 1& 1\\ 0& 2& 1& 0\\ 0& 1& 2& 3 \end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brrrr%7D+2%26+1%26+3%26+1%5C%5C+1%26+0%26+1%26+1%5C%5C+0%26+2%26+1%26+0%5C%5C+0%26+1%26+2%26+3+%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
Penyelesaian :
dengan menggunakan kolom pertama pada matriks B sebagai kofaktor dan berdasarkan Teorema diatas dengan mengambil i = 1, 2, 3, 4 dan j = 1 maka diperoleh.
det(B) = 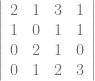
= a11C11 + a21C21 + a31C31 – a41C41
= a11(-1)1+1M11 + a21(-1)2+1M21 + a31(-1)3+1M31 + a41(-1)4+1M41
= a11M11 – a21M21 + a31M31 + a41M41
= 2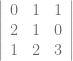 – 1
– 1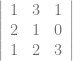 + 0
+ 0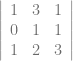 – 0
– 0
hitung lagi determinan untuk matriks 3×3 nya
=
2[ambil i = 1 dan j = 1, 2, 3] – 1[ambil i = 1, 2, 3 dan j = 3] {untuk
matriks ketiga dan keempat tidak perlu dihitung karena koefesiennya 0,
sehingga apabila dikali, hasilnya akan tetap = 0}
= 2[a11C11 + a12C12 + a13C13] – 1[a13C13 + a23C23 + a33C33] + 0 – 0
= 2[a11(-1)1+1M11 + a12(-1)1+2M12 + a13(-1)1+3M13] - 1[a13(-1)1+3M13 + a23(-1)2+3M23 + a33(-1)3+3M33]
= 2[a11M11 – a12M12 + a13M13] – 1[a13M13 + a23M23 + a33M33]
= 2(0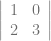 – 1
– 1 + 1
+ 1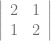 ) – 1(1
) – 1(1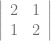 – 0
– 0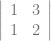 + 3
+ 3 )
)
= 2(0[1(3)-2(0)] – 1[2(3)-1(0)] + 1[2(2)-1(1)]) – 1(1[2(2)-1(1)] – 0[1(2)-1(3)] + 3[1(1)-2(3)])
= 2(0 – 6 + 3) – 1(3 – 0 + 3(-5))
= -6 + 12
= 6






ane punya saran gan. ngeliat tulisannya agak pusing. coba gantti font atau warna nya ^^