Misal kita punya dua buah vektor yaitu a dan u yang berada pada ruang yang sama seperti terlihat pada gambar dibawah ini.
Jika vektor u dan a ditempatkan sedemikian sehingga titik awalnya berimpit dan vektor u disusun dari dua vektor yang saling tegak lurus yaitu w1 dan w2, sehingga vektor u dapat dituliskan sebagai u = w1 + w2. Kemudian vektor a terletak sejajar dengan w1, sedemikian sehingga w1 = ka. Jika kita lihat vektor w1 pada gambar diatas maka vektor w1 diperoleh dari proyeksi ortogonal u terhadap a dan dapat ditulis sebagai w1 = ka, w1 disebut proyeksi ortogonal u pada a [ditulis : proyau] atau dinamakan komponen vector u sepanjang a, sedangkan w2 disebut komponen vektor u yang ortogonal terhadap a. Nilai k ini akan menentukan arah dan panjang dari w1. Jika sudut antara u dan a adalah tumpul , maka tentunya nilai k akan negatif ini juga berarti arah w1 akan berlawanan dengan arah a [perhatikan gambar diatas].
Bagaimana menghitung proyeksi ortogonal u pada a [proyau] dan komponen vektor u yang ortogonal terhadap a [u - proyau] ? Berikut teorema yang memberikan rumus proyau dan u – proyau.
Teorema :
Jika u dan a adalah vektor di ruang-2 atau ruang-3 dan jika a 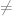 0, maka
0, maka
proyau = 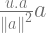
u – proyau =  –
– 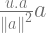
Bukti :
Misalkan w1 = proyau dan w2 = u – proyau.
Dengan menggunakan Hasil Kali Titik, maka diperoleh
u.a = (w1 + w2).a
= w1.a + w2.a
Karena a dan w2 ortogonal, maka diperoleh
= w1.a
= 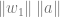 cos
cos 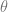
karena a dan w1 sejajar, sehingga 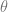 = 00
= 00
= 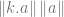 cos 00
cos 00
= k
k = 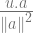
karena proyau = w1 = ka, sehingga diperoleh
proyau = 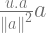

contoh :
Carilah proyeksi ortogonal dari u pada a dan komponen vektor u yang orthogonal ke a.
-
u = (2, 1), a = (-3, 2)
u.a = (2, 1).(-3, 2)
= 2(-3) + 1(2)
= -6 + 2
= -4
= (-3)2 + 22
= 9 + 14
= 13
proyau =
=(-3, 2)
= (12/13, -8/13)
w2 = u – proyau
= (2, 1) – (12/13, -8/13)
= (14/13, 21/13)
-
u = (-7, 1, 3), a = (5, 0, 1)
u.a = (-7, 1, 3). (5, 0, 1)
= -7(5) + 1(0) + 3(1)
= -35 + 0 + 3
= -32
= (5)2 + 02 + 12
= 25 + 0 + 1
= 26
proyau =
=(5, 0, 1)
= (-80/13, 0, -16/13)
w2 = u – proyau
= (-7, 1, 3) – (-80/13, 0, -16/13)
= (-11/13, 1, 55/13)
Sumber :
Anton, H., 1992, Aljabar Linier Elementer, Erlangga, Jakarta.
Anton, H. and Rorres, C., 2005, Elementary Linear Algebra with Applications, John Wiley & Sons, USA.





