Twitter

Klik Like/ikuti

Hasil Kali Titik pada Vektor (Dot Prdoduct)

Author Unknown - -
Home » » Hasil Kali Titik pada Vektor (Dot Prdoduct)

Definisi :
Jika u dan v adalah vektor-vektor di ruang-2 dan ruang-3 dan 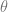\theta adalah sudut diantara u dan v, maka hasil kali titik (dot product) atau hasil kali dalam Euclidis (Euclidean inner product) u.v didefinisikan oleh
u.v = \left\{\begin{matrix} \left \| u \right \| \left \| v \right \| cos \theta, \quad jika \quad u \neq 0 \quad dan \quad v \neq 0 \\ 0, \quad jika \quad u=0 \quad dan \quad v=0 \end{matrix}\right.
\left \| u \right \| artinya panjang vektor u dan didefinisikan sebagai \left \| u \right \| = \sqrt{u_1^2+u_2^2} (jika di ruang-2) dan \left \| u \right \| = \sqrt{u_1^2+u_2^2+u_3^2} (jika di ruang-3). Panjang sebuah vektor juga dikenal dengan nama norma. Secara geometris dapat dilukiskan seperti pada gambar dibawah ini.
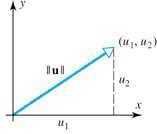
Photobucket
Gambar 1 : vektor pada ruang-2
Jika kita perhatikan, vektor u yang melalui titik asal tersebut membentuk segitiga siku-siku terhadap sumbu-x. Kita bisa memanfaatkan Rumus Pythagoras yaitu \left \| u \right \|^2 = u12 + u22 \Rightarrow \left \| u \right \| = \sqrt{u_1^2+u_2^2}
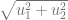
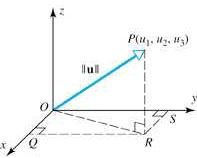
Photobucket
Gambar : vektor pada ruang-3.
Dengan memanfaatkan Rumus Phytagoras juga, diperoleh
\left \| u \right \|^2 = (OR)2 + (RP)2
= (RS)2 + (OS)2 + (RP)2
= (OQ)2 + (OS)2 + (RP)2
= u12 + u22 + u32
\left \| u \right \| = \sqrt{u_1^2+u_2^2+u_3^2}
Penting untuk diketahui juga bahwa sifat – sifat pada perkalian titik vektor dibawah ini :
Misalkan u, v dan w adalah vektor di ruang-2 atau ruang-3 dan k adalah skalar, maka
  1. v.v = \left \| v \right \|^2 yakni \left \| v \right \| = (v.v)1/2
    Bukti :
    Karena vektor v berimpit dengan vektor v itu sendiri maka \theta adalah sudut diantara v dan v adalah 00, diperoleh
    v.v = \left \| v \right \| \left \| v \right \| cos \theta
    = \left \| v \right \|^2 cos 0
    = \left \| v \right \|^2
  2. Jika u dan v adalah vektor – vektor taknol dan \theta adalah sudut di antara kedua vektor tersebut, maka
    \theta lancip jika dan hanya jika u.v > 0
    \theta tumpul jika dan hanya jika u.v < 0
    \theta = \frac{\pi}{2} jika dan hanya jika u.v = 0
    Bukti :
    Perlu diingat bahwa \theta akan lancip jika dan hanya jika cos \theta > 0, \theta akan tumpul jika dan hanya jika cos \theta < 0 dan \theta akan = \frac{\pi}{2} (siku-siku) jika dan hanya jika cos \theta = 0
    Karena \left \| u \right \| > 0 dan \left \| v \right \| > 0 serta berdasarkan Definisi Dot Product bahwa u.v = \left \| u \right \| \left \| v \right \| cos \theta, maka u.v memiliki tanda sama dengan cos \theta.
    Karena 0 \leq \theta \leq \pi, maka sudut \theta lancip jika dan hanya jika cos \theta > 0, \theta tumpul jika dan hanya jika cos \theta < 0, dan \theta = \frac{\pi}{2} jika dan hanya jika cos \theta = 0
  3. u.v = v.u
    Bukti :
    u.v = (u1, u2, u3).(v1, v2, v3)
    = (u1 v1 + u2 v2 + u3 v3)
    = (v1 u1 + v2 u2 + v3 u3) [komutatif bil.riil]
    = (v1, v2, v3).(u1, u2, u3)
    = v.u
  4. u.(v + w) = u.v + u.w
    Bukti :
    u.(v + w) = (u1, u2, u3).[(v1, v2, v3) + (w1, w2, w3)]
    = (u1, u2, u3).(v1 + w1, v2 + w2, v3 + w3)
    = (u1[v1 + w1] + u2[v2 + w2] + u3[v3 + w3])
    = ([u1v1 + u1w1] + [u2v2+ u2w2] + [u3v3 + u3w3]) [distributif bil.riil]
    = ([u1v1 + u2v2 + u3v3] + [u1w1 + u2w2 + u3w3])
    = (u1v1 + u2v2 + u3v3) + (u1w1 + u2w2 + u3w3)
    = u.v + u.w
  5. k(u.v) = (ku).v = u.(kv)
    Bukti :
    k(u.v) = k[(u1, u2, u3).(v1, v2, v3)]
    = k(u1 v1 + u2 v2 + u3 v3)
    = (k[u1 v1] + k[u2 v2] + k[u3 v3])
    = ([ku1]v1 + [ku2]v2 + [ku3]v3) [asosiatif bil.rill]
    = (ku).v
    = (u1[kv1] + u2[kv2] + u3[kv3]) [komutatif bil.riil]
    = u.(kv)
  6. v.v > 0 jika v \neq 0 dan v.v = 0 jika v = 0
    Bukti :
    Karena v \neq 0 berakibat \left \| v \right \| = \sqrt{v_1^2+v_2^2+v_3^2} > 0, sehingga v.v = \left \| v \right \|^2 > 0
    Karena v = 0 berakibat \left \| v \right \| = \sqrt{v_1^2+v_2^2+v_3^2} = \sqrt{0^2+0^2+0^2} = 0, sehingga v.v = \left \| v \right \|^2 = 0
Sumber :
Anton, H., 1992, Aljabar Linier Elementer, Erlangga, Jakarta.
Anton, H. and Rorres, C., 2005, Elementary Linear Algebra with Applications, John Wiley & Sons, USA.