Twitter

Klik Like/ikuti

Penurunan Rumus Jarak Titik ke Garis

Author Unknown - -
Home » » Penurunan Rumus Jarak Titik ke Garis

Jika kita diberikan titik koordinat P0 = (x0, y0) dan persamaan garis ax + by + c = 0 seperti pada gambar diatas, berapa jarak D dari titik koordinat ke garis tersebut? Untuk menghitung kita membutuhkan rumus dan rumus yang digunakan adalah D = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} . Pertanyaannya sekarang, darimana asal rumus tersebut? Ok, sekarang saya akan mencoba menjabarkan penurunan rumus untuk jarak D tersebut.
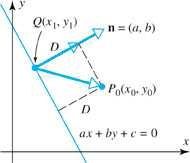PhotobucketPerhatikan gambar diatas. Misal kita punya sebarang titik yang terletak pada garis yaitu Q(x1, y1) dan vector n = (a, b) sedemikian sehingga titik awalnya terletak pada Q dan vektor n tegak lurus dengan garis. Dari gambar terdapat,
\vec{QP_0} = (x0 – x1, y0 – y1)
\vec{QP_0} .n = a(x0 – x1) + b(y0 – y1)
\left \| n \right \| = \sqrt{a^2+b^2}
Seperti yang terlihat pada gambar bahwa jarak D sama dengan panjang proyeksi ortogonal \vec{QP_0} pada n. Sehingga dari rumus proyeksi vektor pada tulisan sebelumnya, diperoleh
D = \left \| proy_n \vec{QP_0} \right \|
= \frac{|\vec{QP_0}.n|}{\left \| n \right \|}
= \frac{|a(x_0-x_1)+b(y_0-y_1)|}{\sqrt{a^2+b^2}}
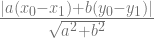
Karena titik Q(x1, y1) terletak pada garis tersebut, maka koordinatnya akan memenuhi persamaan garis sehingga
= \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} dengan c = -ax1 – by1
Sumber :
Anton, H., 1992, Aljabar Linier Elementer, Erlangga, Jakarta.
Anton, H. and Rorres, C., 2005, Elementary Linear Algebra with Applications, John Wiley & Sons, USA.